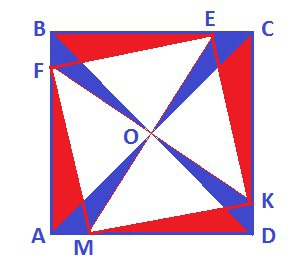
Диагонали АС и BD - равны и перпендикулярны.
Продолжаем прямые OF и OE до пересечения с противоположными сторонами и получаем перпендикулярные прямые FK и ME.
Получаем секущую прямую между двумя параллельными сторонами.
Четыре треугольника - равны - AFM, BEF, CKE, DMK.
Значит равны и их гипотенузы - стороны четырехугольника FEKM.
Получили фигуру - стороны равны, диагонали и равны и перпендикулярны - фигура = квадрат.